I am an applied mathematician primarily interested in real-life problems whose treatment requires analysis of a model / justification of the approximation or those that can be effectively tackled with analytical tools such as asymptotic methods or closed-form solution reducibility.

I enjoy learning new things while working on diverse subjects analysing a problem, devising a constructive solution approach and verifying / implementing it numerically. Current and past topics of my research include:

• wave propagation in porous media (fluid / solid inclusion scattering for Biot elastodynamics equations);
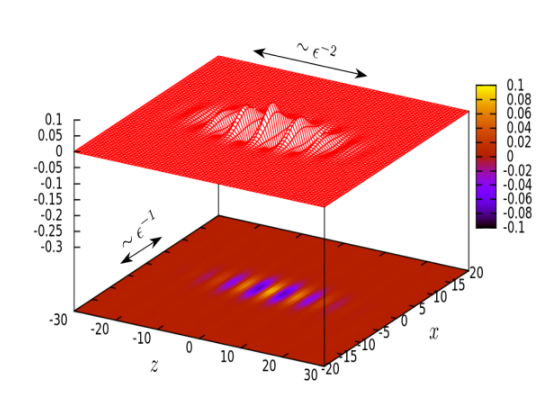
• nonlinear PDEs (analysis of one NLS model for laser beams in photopolymers; Darboux transformation);
• approximation theory (approximation of square-integrable functions by traces of analytic functions with certain properties such as pointwise constraints);
• integral equations and optimal bases construction (spectral theory for compact one-dimensional self-adjoint integral operators with convolution kernels);
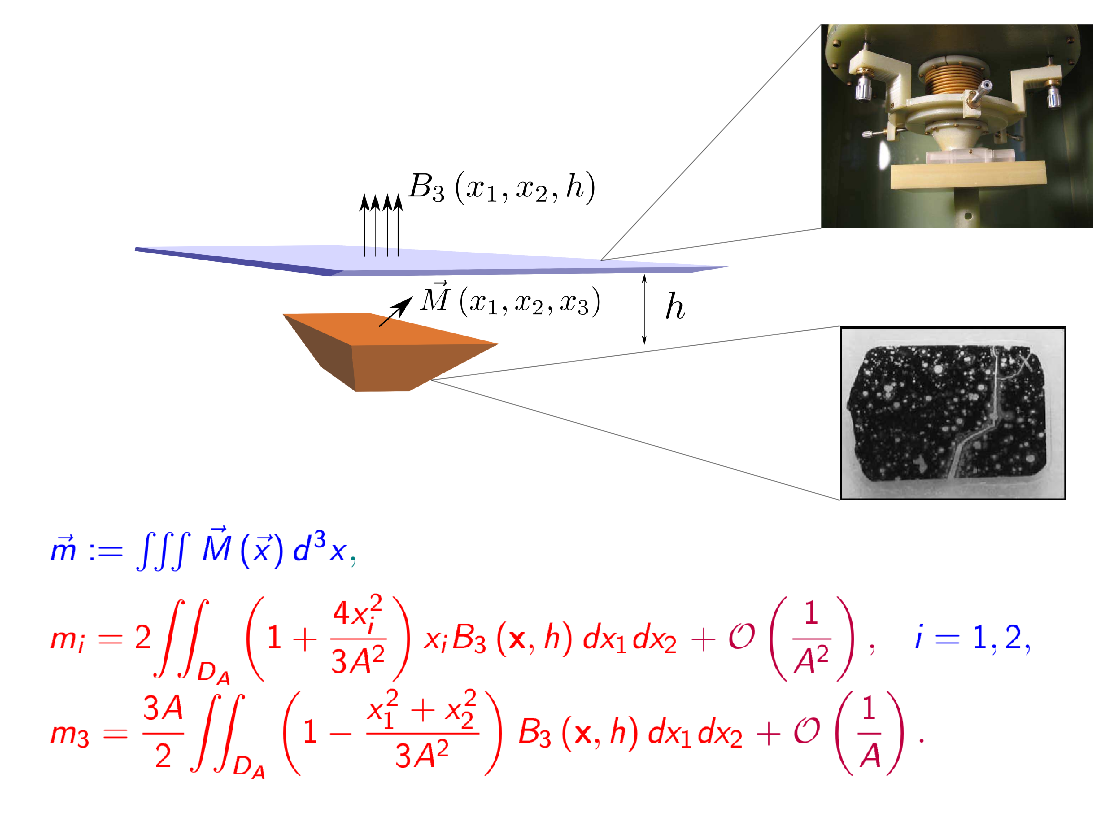
• inverse magnetisation problem (analytical estimation of net magnetisation moment components from partial measurements of magnetic field);
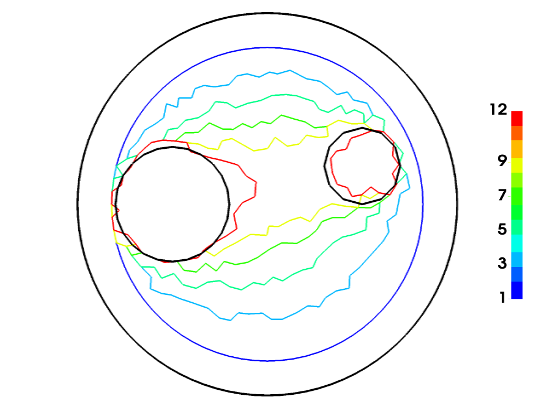
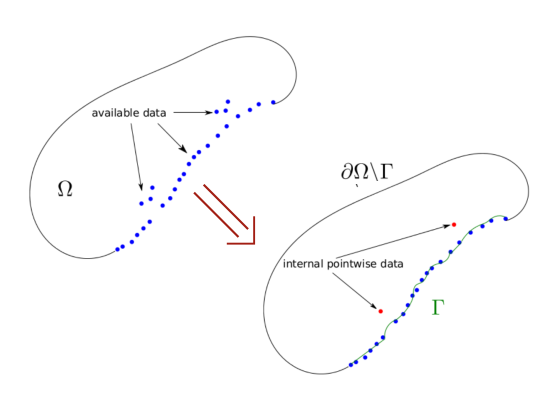
• inverse obstacle problem (determining domain geometry for transient wave equation from partial Dirichlet+Neumann data);
• efficient solution of the Helmholtz equation (asymptotic-numerical methods for high-frequency wave propagation in homogeneous and heterogeneous media);
• long-time behaviour analysis for solutions of wave equations (extension of the limiting amplitude principle and decay problems in unbounded domains);
• contact-mechanical problems (integral equation approach; development, solution and analysis of a new model for wear in the punch-sliding problem).

I obtained my Ph.D. degree from the University of Nice Sophia Antipolis (now Côte d'Azur University) in 2016, with a doctoral thesis written at INRIA Sophia Antipolis Méditerranée, France. My thesis work under supervision of Juliette Leblond and Laurent Baratchart was dedicated to the mathematical study of some inverse problems for the Laplace and Poisson equations, in both abstract and concrete settings.
Before that, I did my "specialist" program at Moscow Engineering Physics Institute MEPhI (Faculty of Theoretical and Experimental Physics), Russia, followed by 2 M.Sc. degrees: from the international EU Erasmus Mundus program MathMods (now InterMaths) in 2010, and McMaster University (Department of Mathematics & Statistics), Canada, in 2012, with a M.Sc. thesis work on the analysis of nonlinear wave propagation in photopolymers written under supervision of Dmitry Pelinovsky.
After my Ph.D., from 2016 to 2018, I was a post-doc at ENSTA Paris (France) working with Laurent Bourgeois on the inverse obstacle problem for the time-domain wave equation with constant coefficients.
Since 2018, I have been employed by Institute of Analysis & Scientific Computing at Technical University of Vienna (TU Wien), Austria, as a research postdoc, working in the group of Anton Arnold (in collaboration with Ilaria Perugia and Sjoerd Geevers from University of Vienna), on different aspects of linear wave propagation.
In 2022, I have been on a partial teaching contract at TU Wien, see the "Teaching" section for more details.
From 2019 to 2024, I was also affiliated with the St. Petersburg Department of Steklov Mathematical Institute of Russian Academy of Sciences as a permanent researcher on unpaid leave.
Since October 2022, I hold ISFP (Inria Starting Faculty Position) at Centre Inria d'Université Côte d'Azur as a member of the FACTAS research team working on inverse problems.

You can contact me by email: dmvpon@gmail.com / dmitry.ponomarev@inria.fr, or find me at:
Office B.222, FACTAS team, Centre Inria d'Université Côte d'Azur, 2004 Route des Lucioles, 06902 Biot, France.